おばあちゃんの宅配便で数学が大好きに
立川吉笑
毎週水曜日恒例、談笑一門でのまくら投げ。今週のお題は「おばあちゃん」。前回担当の笑二から重たいまくらが飛んできて、まだ腕がジーンとしているなか次の師匠へつなぎたい。
僕は昔から数学が好きで、論理から組み立てるネタ作りの方法は落語にも反映されている気がする。

「勉強」や「学問」自体がそういう風に思われがちだけど、特に「数学」はそれだけで「難しいモノ」だとか「ネガティブなモノ」だとか、多くの方から敬遠されている気がしていて、そんな風潮が僕はとても嫌いだ。「知らないことを知る」ということを楽しめるのなら、たちまち「学問」は「娯楽」と化す。
そんな思いから、各分野の専門家を講師にお招きする『吉笑ゼミ。』というイベントを自主開催していて、次回のゼミは8月10日に開講しますよ、というのはただの告知。
今回は僕が数学を好きになったきっかけについて書いてみよう。それまでも数学は好きだったけど、あるできごとをきっかけに僕は数学の虜(とりこ)になったのだ。
大学1年生の頃、京都の八坂神社近くのローソンでアルバイトをしていた。週2回の深夜勤で得られる給料は、実家暮らしの僕にとっては十分すぎるものだった。
22時から始まる深夜勤。明け方になると体はけだるく、頭はぼーっとしてくる。布団に入ったら3秒で寝られる、そんな朦朧(もうろう)とした時間帯にある日、一人のおばあちゃんが宅配サービスを利用しにやってきた。
箱のサイズを計って、送り先を入力し、料金を受け取ると、僕は所定の位置に預かった荷物を置いた。外の空気を吸おうと、店の外までおばあちゃんを見送りに出たらふいに、
「これって、どんな箱で送ったら一番得かなぁ?」
と聞かれた。とっさに僕は
「立方体です」
と答えた。
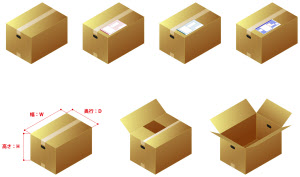
取り扱っている宅配サービスの値段は、荷物の重さじゃなくて、箱の大きさ(縦と横と高さの和)で決まっていた。3辺の和が60cm以内なら「60サイズ」、80cm以内なら「80サイズ」という仕組みだ。
ほんの少し数学を勉強していると、そういった場合はだいたい均等な形が一番効率的だと感覚的に知っているから、僕はふいの質問に3辺の長さが等しい立方体が一番容量が大きいと即答した。もしかしたら球とか、もっと他の形が一番容量が大きくなる可能性もあるけど、それはもう僕やおばあちゃんの範ちゅうを超えている。
「ありがとう」
と言って、明け方の東大路通を歩いていくおばあちゃんを見送りながら、
「本当にそうか?」
と心配になった。うそを教えてしまったかもしれない。
店内に戻ると捨てられたレシートの裏を使って計算し始めた。
例えば3辺の和が60cm以内という条件の60サイズの場合で考えると、縦10cm・横20cm・高さ30cmの直方体の体積は6000立方cm。一方で、縦・横・高さが20cmの立方体の体積は8000立方cmとなり、やっぱり立方体が一番多く入る計算になる。
「やっぱりそうだったか」
と普通はそこで納得するものかもしれないけど、数学好きの端くれとしては
「本当にそうなのか?」
とさらに疑問を抱く。
だから今度は、縦をXcm、横をYcm、高さをZcmと置いて、果たして体積XYZ立方cmの最大値がどうなるのか、ということについて考え始めた。
60サイズのときについて考えているから、数学の問題っぽく整理すると、
(ただし、X>0,Y>0,Z>0とする)
となる。
(ここらで読者の方が次第に離れていく様子が目に見えるけど、実際はめちゃくちゃ簡単なことが書かれているだけですから、思考ストップせずに付き合ってもらいたいです!)
当時の僕の数学力は、大学受験レベルの数学を少し勉強している程度。全く勉強してこなかったというわけではないけど、特に点数が高かったわけでもなく、たぶん平均点くらいの位置づけだったように思う。
その程度の僕がこの問題に直面すると解き方はシンプルで、まずは「X+Y+Z=60」を変形して「X=60-Y-Z」という式を作って、あとはそれをXYZに代入してゴリゴリ計算をしていって、解けるか解けないか命運を託す、というもの。
上記を代入してみると、出来上がる式はYとZの2次式になる。
少し複雑になるから細かい計算過程は省くけど、特に役立つのは高校で習ったばかりの微分法で、上記の式を「Yの関数として」と「Zの関数として」の2パターンで考えて、微分して、増減表を書いて、それをもとにグラフを書いて判断したら、すぐに「X=Y=Zのとき、XYZが最大になる」ということが分かった。
このあたりになってくると自分でも本質を完全に理解しているかと聞かれると自信はないけど、受験勉強を少しやった方にとっては、何か関数があったら「微分して増減表を書いてグラフの形を把握する」というのは定番中の定番みたいな方法だ。
料理をする人が、「昆布でだしをとる場合は水のときから入れておくけど、かつお節のときは沸騰してから入れる」と使い分けるくらいの感覚で、少し高校数学を勉強した人はごく自然に上記のように解き進めることになる。
おばあちゃんを見送って30分後、上記の計算からみごとに証明を終えてホクホクしたまま自転車で家に帰る。その道中でふと思うことがあった。

「もっと簡単に解ける気がするんだけどなぁ」
僕は全然そのレベルじゃなかったけど、数学好きの強者は同じ問題を解くにしてもよりエレガントな解法を好む。上記みたいにゴリゴリ解き進める方法はエレガントさのかけらもない。そういう友達がまわりに何人かいたおかげで僕も何となくエレガントな解法に憧れを抱くようになっていた。
「彼らだったらもっと別の解法を見つけるはずだ」
それから奇妙な数日が始まった。
誰に頼まれた訳でもないのに、ずっと頭のなかに
(ただし、X>0,Y>0,Z>0とする)
という問題がちらついて仕方ないのだ。気分はいっぱしの数学者になったつもりで、何か解法の糸口を思いついてはノートに書くようになった。
上記の問題に対して、僕は一つの直感を持っていた。それは高1の時にならった「相加・相乗平均の大小関係」というものだ。
A>0,B>0のとき、A+Bを2で割った「足した時の平均」と、A×Bをルートの中に入れた「掛け合わせたときの平均」は
「足した時の平均」≧「掛け合わせたときの平均」が必ず成り立つ。
というテクニック。言葉で表すとややこしいけど、要するに「A+B」と「AB」の大小関係が一発で判別できる便利な武器が「相加・相乗平均の大小関係」で、この関係式を応用できるような気がした。
「相加・相乗平均の大小関係」で先生から口うるさく言われたのは「A>0,B>0」のときにしか、この公式は使えないということ。つまり裏を返せば問題文に「A>0,B>0」という条件が示してあれば、「相加・相乗平均の大小関係」を使うことが多いということになる。
いま、おばあちゃんから出題された宅配便問題はX,Y,Zとも長さだから0より大きい。そして式に出てくるのはX+Y+ZとXYZだから、これは「相加・相乗平均の大小関係」を使える感じがビンビンに伝わってくる。
ただ、高校で習ったのは変数がAとBの2次までで、これがAとBとCの3変数でも成り立つかは分からないということ。もし「相加・相乗平均の大小関係」が3変数でも成り立つことが証明できれば、おばあちゃんの宅配便問題は一発で解けることになる。
おばあちゃんが店に来てから3日後、僕は「相加・相乗平均の大小関係」が3変数でも成り立つかを証明することになった。
この証明は驚くほど簡単だった。それこそゴリゴリ計算をしたらすぐに証明できてしまって、僕はおばあちゃんの宅配便問題を即答できる強力な武器を手に入れた。
こうなると、もう少し先まで確かめたくなるのが好奇心旺盛な僕だ。
いま、3変数まで「相加・相乗平均の大小関係」が成り立つことは証明したけど、こうなったらN変数でも成り立つのか証明したくなってしまう。
A+B+C+…とN個の変数の和をNで割った相加平均と、A×B×C×…とN個の変数の積のN乗根である相乗平均でも、「足した時の平均」≧「掛け合わせたときの平均」が成り立つのか、証明しようじゃないか。
そこからの日々は壮絶なものだった。
この問題は正直めちゃくちゃ難しかった。
得意のパワープレー、ゴリゴリと計算しようとしても複雑すぎて、すぐにページが埋まってしまう。N乗根を失くすために両辺をN乗したら、右辺はすっきりするけど、今度は左辺がめちゃくちゃ複雑になってしまう。
高校時代に習った証明の強力な道具である数学的帰納法も使った。N=kのときに成立すると仮定した時にN=k+1でも成立するか、どうか。条件を書くだけでもノートが埋まり切ってしまう。
それじゃあ背理法はどうか。条件が成り立たないと仮定すると何か不具合が起きるのか? 考えてもさっぱりわからない。
気がつくとおばあちゃんが来店してから一週間近く経っていた。
何で、こんな誰にも求められていない問題について真剣になっているのかわからないけど、山に登り始めた以上もう僕には引き返すことはできなかった。それはさながら未解決問題に挑み続ける数学者と全く同じだった、自分の中では。
どれだけ挑んでも自分の力では解けない。そもそも解き方の糸口すらつかめない。
完全に心が折れかけていた8日目、何かヒントはないかと高校時代に使っていた参考書をペラペラめくっていると、それはあった。
なんと上記と全く同じ問題、すなわち『「相加・相乗平均の大小関係」がN変数でも成り立つことを証明せよ』という問題がある年の滋賀県立医大の入試問題に出題されていたのだ。
その瞬間、体に大きな衝撃が走った。
高校時代、「何でこんなことを勉強させられているんだろう?」としばしばむなしく感じることがあった。「相加・相乗平均の大小関係」なんて生きていく上で役に立たないだろうと思っていたけど、違った。
「相加・相乗平均の大小関係」はいかに宅配便を効率的に利用するかを調べるために必要な知識だったんだ!
あまりに抽象的だと思っていた数学が、実はとても身近なところに関係しているのだと知った。だって、「相加・相乗平均の大小関係」が近所のおばあちゃんとつながっていたのだから。
それで僕は数学が好きになった。
あたりを見回すと、様々なものが目に入る。机、水道、風。本、これを書いているパソコン、雲。貧乏ゆすり、シャワー、包丁。その全てに、僕の知らない何かが隠されているだろう。そもそも僕には知らないことが多すぎる。
知らないことを知る。それを娯楽と思えるならば、たちまち生きていくことが楽しくなる。
(次回7月6日は立川談笑師匠の登場予定です)

ワークスタイルや暮らし・家計管理に役立つノウハウなどをまとめています。
※ NIKKEI STYLE は2023年にリニューアルしました。これまでに公開したコンテンツのほとんどは日経電子版などで引き続きご覧いただけます。
















